计算几何-线线相交
线线相交
几何图元中定义的线包括: 线段(LineSegment2), 圆(Circle2), 圆弧(Arc2), 直线(Line2), 射线(Ray2), 本文中的线线相交包含以下几种情况:
line_segment_2_line_segment_2_intersection: 线段与线段相交line_segment_2_circle_2_intersection: 线段与圆相交line_segment_2_arc_2_intersection: 线段与圆弧相交line_segment_2_line_2_intersection: 线段与直线相交line_segment_2_ray_2_intersection: 线段与射线相交circle_2_circle_2_intersection: 圆与圆相交circle_2_arc_2_intersection: 圆与圆弧相交arc_2_arc_2_intersection: 圆弧与圆弧相交line_2_line_2_intersection: 直线与直线相交line_2_ray_2_intersection: 直线与射线相交
线段与线段相交
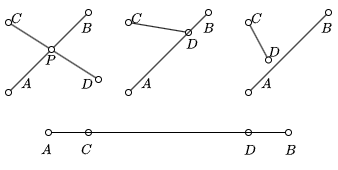
线段与线段相交的情况有以下几种:
- 有一个交点: 交点不是线段的端点
- 有一个交点: 交点是线段的端点
- 没有交点
- 有两个交点: 交点是线段的端点
线段与线段 重叠(overlap) 是特殊情况, 本文中认为 overlap 相交, 交点是线段的端点
- 初始化存储交点的数组
- 使用
叉乘判断是否相交:
- 线段
AB与线段CD相交, 且交点不是线段的端点, 端点C和端点D位于线段AB两侧, 所以叉乘的结果为负数 - 线段
AB与线段CD相交, 且交点是线段的端点, 叉乘的结果为 0 - 线段
AB与线段CD不相交, 端点C和端点D位于线段AB同一侧, 叉乘的结果为正数 - 线段
AB与线段CD重叠, 叉乘的结果为 0
- 如果相交, 判断端点是否在另一条线段上, 如果在, 则添加到交点数组中
- 如果交点数组不为空, 则返回交点数组, 结束
- 如果交点数组为空, 则说明交点不是端点, 计算交点
线段
AB上的任何点可以表示为:
线段CD上的任何点可以表示为:
两条线段相交时, 有: , 即: , 解方程得到交点
两边同时叉乘 , 得到:
所以 , 代入 , 得到交点
线段与圆相交
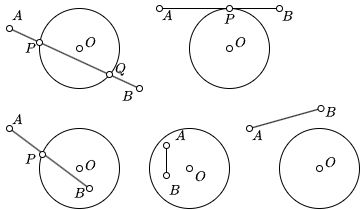
线段与圆相交的情况有以下几种:
- 有两个交点: 圆心到线段的距离小于半径, 线段端点都不在圆内
- 有一个交点: 圆心到线段的距离等于半径
- 有一个交点: 圆心到线段的距离小于半径, 一个端点在圆内, 一个端点在圆外
- 没有交点: 圆心到线段的距离大于半径且线段端点都在圆外,或者圆心到线段的距离小于半径, 两个端点都在圆内
- 先判断线段的端点与圆的位置关系
如果两个端点都在圆内, 则没有交点, 结束
如果两个端点都在圆上, 则有两个交点, 结束 - 如果两个端点至少有一个在圆内(必定是一个在圆内, 另一个在圆上或圆外)
设圆内的点为 , 另一个点为 , 构造直线 过 和 , = ( 为 的归一化)
求圆心 投影到 上的点 , 毕达哥拉斯定理求交点 与 的距离
= - 两个端点至少有一个在圆外(必定是一个在圆外, 另一个在圆外或圆上)
构造直线 过 和 , = ( 为 的归一化)
求圆心 投影到 上的点 , 毕达哥拉斯定理求交点 与 的距离
= , =
如果 在线段上, 则 为交点
线段与圆弧相交
线段与圆弧相交的情况与圆类似, 区别在于线段与圆弧相交时, 交点可能在圆弧的起点和终点之间, 也可能在圆弧的起点和终点之外. 因此, 需要判断交点是否在圆弧上.
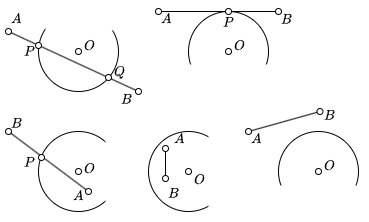
- 获取线段与圆的交点
- 判断交点是否在圆弧上
线段与直线相交
将线段构造成直线, 判断直线与直线的交点是否在线段上, 重叠情况认为有两个交点, 具体实现见下文.
线段与射线相交
将线段构造成直线, 判断直线与射线的交点是否在线段上, 重叠情况认为有两个交点, 具体实现见下文.
圆与圆相交
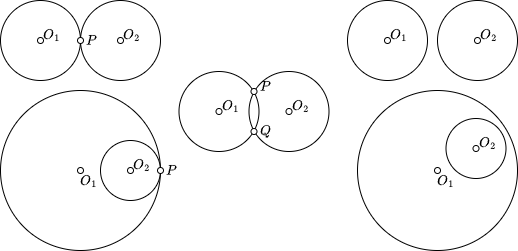
圆与圆相交的情况有以下几种:
- 有两个交点: 两圆的圆心距小于两圆的半径之和, 且大于两圆的半径之差
- 有一个交点: 内切或外切, 两圆的圆心距等于两圆的半径之和或之差
- 没有交点: 内含或外离, 两圆的圆心距大于两圆的半径之和或之差
- 圆心和半径相同(overlap)是特殊情况, 本文中认为 overlap 不相交
- 计算两圆的圆心距 , 两圆半径分别为 和 , 半径之和 , 半径之差的绝对值
- 如果 , 不相交, 结束
- 如果 , 外切, 有一个交点, 结束
- 如果 , 内切, 有一个交点, 结束
如果 : ,
如果 : , - 如果 且 , 有两个交点, 结束
直线 垂直平分 线段 , 根据余弦定理求解 的长度, 进而求解交点
- 没有交点, 结束
圆与圆弧相交
先求圆与圆的交点, 再判断交点是否在圆弧上, 圆心和半径相同(overlap)不相加.
圆弧与圆弧相交
先求圆与圆的交点, 再判断交点是否都在两个圆弧上, 圆心和半径相同(overlap)不相加.
直线与直线相交
直线与直线相交的情况有以下几种:
- 有一个交点: 两直线相交
- 不相交: 两直线平行或重合
直线的一般方程为: , 两直线相交时, 有: , , 解方程得到交点.
= , 如果 = , 两直线平行或重合, 否则有一个交点.
=
=
直线与射线相交
先求直线与直线的交点, 再判断交点是否在射线上, overlap 不相交.
