点线投影

几何图元中定义的线包括: 线段(LineSegment2), 圆(Circle2), 圆弧(Arc2), 直线(Line2), 射线(Ray2), 本文中的点线投影包含以下几种情况:

  • point_2_line_segment_2_projection: 点到线段的投影
  • point_2_line_2_projection: 点到直线的投影
  • point_2_ray_2_projection: 点到射线的投影

点线投影

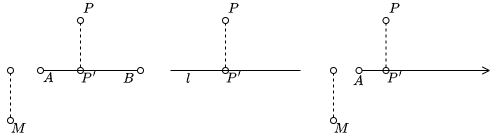
点到线段的投影

点 PP 到线段 AB 的投影是线段 AB上的一个点 P′P^{\prime}, 使得 PP′PP^{\prime} 垂直于AB, 且 P′P^{\prime} 在AB上.

  1. 计算 AP→\overrightarrow{AP} 在 AB→\overrightarrow{AB} 上的投影比例 tt:

    vv = AP→⋅AB→\overrightarrow{AP} \cdot \overrightarrow{AB}
    ww = AB→⋅AB→\overrightarrow{AB} \cdot \overrightarrow{AB}
    如果 vv < 00 或者 vv > ww, 则说明 P′P^{\prime} 不在 AB 上, 结束
    tt = vw\frac{v}{w}

  2. 计算 P′P^{\prime} 的坐标:
    P′P^{\prime} = A+t⋅AB→A + t \cdot \overrightarrow{AB}

点到直线的投影

直线 ll 的一般方程为: Ax+By+CAx + By + C = 00

点 P(x0,y0)P(x_0, y_0) 到直线 ll 的投影是直线 ll 上的一个点 P′(x1,y1)P^{\prime}(x_1, y_1), 使得 PP′PP^{\prime} 垂直于 ll.

  1. 如果 BB = 00, 说明直线 ll 为垂直于 xx 轴的直线, 则 P′(−CA,y0)P^{\prime}(-\frac{C}{A}, y_0).

  2. 如果 AA = 00, 说明直线 ll 为垂直于 yy 轴的直线, 则 P′(x0,−CB)P^{\prime}(x_0, -\frac{C}{B}).

  3. 直线 PP′PP^{\prime} 的一般方程为: ABx−y+y0−AB⋅x0\frac{A}{B}x - y + y_0 - \frac{A}{B} \cdot x_0 = 00, 与直线 ll 的交点即为 P′P^{\prime}.

  4. 求解交点 P′P^{\prime} 的坐标:

    A2A_2 = AB\frac{A}{B}
    B2B_2 = −1-1
    C2C_2 = y0−A2⋅x0y_0 - A_2 \cdot x_0
    x1x_1 = −B2⋅C+B⋅C2A⋅B2−A2⋅B\frac{-B_2 \cdot C + B \cdot C_2}{A \cdot B_2 - A_2 \cdot B}
    y1y_1 = A2⋅C−A⋅C2A⋅B2−A2⋅B\frac{A_2 \cdot C - A \cdot C_2}{A \cdot B_2 - A_2 \cdot B}

ToDo: 点到射线的投影