计算几何-凸包

凸包

对于给定的点集, 凸包是一个凸多边形, 该多边形的顶点是点集中的点, 并且点集中的所有点都在这个多边形内部或边上. 在二维空间中, 凸包可想象成一个橡皮圈, 将点集包裹在内部, 凸包用最小的周长包围了给定的所有点.

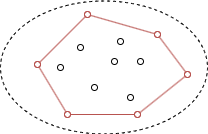
凸包的性质

• 选取凸包的任意一条边, 点集中的所有点都在这条边的一侧或者在边上.
• 选取凸包的任意一个顶点, 从该顶点逆时针遍历凸包的所有顶点, 遍历的边总是向左转的.

Andrew 算法

Andrew 算法是一种求解凸包的算法, 该算法的时间复杂度为 $O(n\log{n})$, 其基本流程如下:

1. 将所有点按照 $x$ 坐标排序, 若 $x$ 坐标相同则按照 $y$ 坐标排序.

   显然排序后的第一个元素和最后一个元素一定在凸包上
   由于逆时针遍历左转, 所以从最左的顶点开始, 逆时针遍历, 所有边都是左转的顶点都是凸包的下半部分, 从最右的顶点开始, 逆时针遍历, 所有边都是左转的顶点都是凸包的上半部分
   使用叉乘判断是否左转

2. 构造一个栈, 存储凸包的下半部分的顶点
3. 从左到右遍历所有点, 一旦发现当前点( $P$ )和栈顶的两个点( $S_1$, $S_2$)不是左转, 则将栈顶的点弹出, 直到栈顶的两个点和当前点构成的向量是左转的.
4. 构造一个栈, 存储凸包的上半部分的顶点
5. 从右到左遍历所有点, 一旦发现当前点( $P$ )和栈顶的两个点( $S_1$, $S_2$)不是左转, 则将栈顶的点弹出, 直到栈顶的两个点和当前点构成的向量是左转的.
6. 合并两个栈(删除上半部分的最后一个顶点和下半部分的最后一个顶点), 得到凸包.