计算几何-点线位置关系

点线位置关系

几何图元参考: 计算几何-几何图元
设有一个二维点 $P$

如果把线段 $AB$ 看作一个有向线段，那么点 $P$ 与线段 $AB$ 之间的位置关系有以下几种情况：

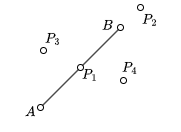
点与线段的四种位置关系

以上四种情况可以分成两类：

点和线段共线

通过点乘运算判断向量的夹角, 进而判断共线关系, 也可以通过叉乘计算有向面积, 判断共线关系.

若 $|\overrightarrow{AB} \cdot \overrightarrow{AP}| = |\overrightarrow{AB}| \cdot |\overrightarrow{AP}|$ , 则 $P$ 与线段 $AB$ 共线
若 $\overrightarrow{AB} \times \overrightarrow{AP} = 0 \leftrightarrow$ $\triangle ABP$ 面积为零 $\leftrightarrow$ 则 $P$ 与线段 $AB$ 共线

共线的情况下:

如果点 $P$ 在线段 $AB$ 上, 显然 $|\overrightarrow{AP}| + |\overrightarrow{BP}| = |\overrightarrow{AB}|$

也可以通过点乘进行判断:

$0 \leq \overrightarrow{AB} \cdot \overrightarrow{AP} \leq \overrightarrow{AB} \cdot \overrightarrow{AB}$

因为如果 $P$ 在 $AB$ 上, 那么 $\overrightarrow{AP}$ 的投影肯定在 $\overrightarrow{AB}$ 上, 且 $0 \le$ 投影长度 $\le |\overrightarrow{AB}|$ .

不共线的情况下:

如果点 $P$ 在线段 $AB$ 的两侧, 显然 $\triangle ABP \neq 0$

点在线段两侧

$A$ , $B$ , $P_3$ 三个顶点逆时针排列, 有向面积为正, $A$ , $B$ , $P_4$ 三个顶点顺时针排列, 有向面积为负

$\overrightarrow{AB} \times \overrightarrow{AP} > 0 \leftrightarrow S_{\triangle ABP} > 0 \leftrightarrow P$ 在 $AB$ 的左侧

$\overrightarrow{AB} \times \overrightarrow{AP} < 0 \leftrightarrow S_{\triangle ABP} < 0 \leftrightarrow P$ 在 $AB$ 的右侧

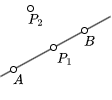
由于直线是无限长的，所以点 $P$ 与直线 $AB$ 之间的位置关系只有两种情况:

直线方程为 $ax + by + c = 0$ , 点 $P(x_0, y_0)$ , 则有:

$ax_0 + by_0 + c = 0 \leftrightarrow$ 点 $P$ 在直线 $AB$ 上
$ax_0 + by_0 + c \neq 0 \leftrightarrow$ 点 $P$ 不在直线 $AB$ 上

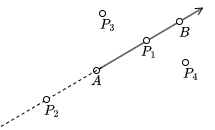
射线是有向的，所以点 $P$ 与射线 $AB$ 之间的位置关系有以下几种情况：

设射线 $AB$ 的起点为 $A$ , 方向为 $\overrightarrow{AB}$

当 $\overrightarrow{AP}$ 和 $\overrightarrow{AB}$ 共线时:

$\overrightarrow{AP} \cdot \overrightarrow{AB} > 0 \leftrightarrow$ 点 $P$ 在射线 $AB$ 上
$\overrightarrow{AP} \cdot \overrightarrow{AB} < 0 \leftrightarrow$ 点 $P$ 在射线 $AB$ 的反向延长线上

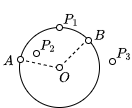
设圆心为 $O$ , 半径为 $r$ , 点 $P$ 与圆之间的位置关系有以下几种情况：

只考虑圆弧是圆的一部分, 圆弧的圆心为 $O$ , 半径为 $r$ , 起点为 $A$ , 终点为 $B$ , 点 $P$ 与圆弧之间的位置关系有以下几种情况：

点 $P$ 在圆弧上: $\angle AOP + \angle POB = \angle AOB and |\overrightarrow{OP}| = r$
点 $P$ 不在圆弧上: $\angle AOP + \angle POB \neq \angle AOB or |\overrightarrow{OP}| \neq r$