向量

默认欧几里得空间.

向量 是既有大小又有方向的量, 在几何中常用有向线段表示, 它的起点和终点分别是两个点, 常用 a⃗\vec{a}、AB→\overrightarrow{AB} 表示, 其中 AA, BB 是向量的起点和终点.

在坐标系中 a⃗=(x,y,...)\vec{a} = (x, y, ...), 其中 x,y,...x, y, ... 是向量的坐标, 向量的维度取决于坐标的个数, 例如二维向量 (x,y)(x, y), 三维向量 (x,y,z)(x, y, z).

向量的模长是向量的长度, 记作 ∣a⃗∣|\vec{a}|, 计算公式为: ∣a⃗∣=x2+y2+...|\vec{a}| = \sqrt{x^2 + y^2 + ...}.

单位向量是模长为 11 的向量, 零向量是模长为 00 的向量.

平行向量或共线向量是方向相同或者相反的向量, 零向量与任何向量都是平行的.

相等向量是指长度相等且方向相同的向量.

向量运算

设有两个二维向量: a⃗=(x1,y1)\vec{a} = (x_1, y_1), b⃗=(x2,y2)\vec{b} = (x_2, y_2)

加法

两个维度相同的向量相加, 相当于将两个向量的坐标分别相加:

a⃗+b⃗=(x1+x2,y1+y2)\vec{a} + \vec{b} = (x_1 + x_2, y_1 + y_2)

向量加法的三角形法则

向量的加法满足交换律和结合律:
交换律: a⃗+b⃗=b⃗+a⃗\vec{a} + \vec{b} = \vec{b} + \vec{a}
结合律: (a⃗+b⃗)+c⃗=a⃗+(b⃗+c⃗)(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})

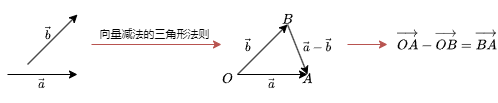
减法

两个维度相同的向量相减, 相当于将两个向量的坐标分别相减:

a⃗−b⃗=(x1−x2,y1−y2)\vec{a} - \vec{b} = (x_1 - x_2, y_1 - y_2)

向量减法的三角形法则

数乘

向量与数相乘, 相当于将向量的坐标分别与数相乘:

k⋅a⃗=(k⋅x,k⋅y)k \cdot \vec{a} = (k \cdot x, k \cdot y)

向量数乘

数乘满足结合律和分配律:
结合律: k⋅(m⋅a⃗)=(k⋅m)⋅a⃗k \cdot (m \cdot \vec{a}) = (k \cdot m) \cdot \vec{a}
分配律: (k+m)⋅a⃗=k⋅a⃗+m⋅a⃗(k + m) \cdot \vec{a} = k \cdot \vec{a} + m \cdot \vec{a}

点乘

两个维度相同的向量相乘, 结果是一个数:

a⃗⋅b⃗=x1⋅x2+y1⋅y2\vec{a} \cdot \vec{b} = x_1 \cdot x_2 + y_1 \cdot y_2

点乘满足交换律和分配律:
交换律: a⃗⋅b⃗=b⃗⋅a⃗\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}
分配律: a⃗⋅(b⃗+c⃗)=a⃗⋅b⃗+a⃗⋅c⃗\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}

在几何中, 点乘的结果是两个向量的模长乘以夹角的余弦值:

a⃗⋅b⃗=∣a⃗∣⋅∣b⃗∣⋅cos⁡θ\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos{\theta}

其中 θ\theta 是两个向量的夹角.

向量点乘

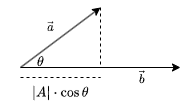
从几何定义可以看出, a⃗⋅b⃗\vec{a} \cdot \vec{b} 可以理解为 a⃗\vec{a} 在 b⃗\vec{b} 方向上的投影长度乘以 b⃗\vec{b} 的模长.

  • a⃗⋅b⃗=0↔a⃗⊥b⃗\vec{a} \cdot \vec{b} = 0 \leftrightarrow \vec{a} \perp \vec{b}
  • a⃗⋅b⃗>0↔a⃗\vec{a} \cdot \vec{b} > 0 \leftrightarrow \vec{a} 与 b⃗\vec{b} 的夹角小于 π2↔\frac{\pi}{2} \leftrightarrow 两个向量的方向相近
  • a⃗⋅b⃗<0↔a⃗\vec{a} \cdot \vec{b} < 0 \leftrightarrow \vec{a} 与 b⃗\vec{b} 的夹角大于 π2↔\frac{\pi}{2} \leftrightarrow 两个向量的方向相反
  • a⃗⋅b⃗=∣a⃗∣⋅∣b⃗∣↔a⃗\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \leftrightarrow \vec{a} 与 b⃗\vec{b} 的夹角为 00
  • a⃗⋅b⃗=−∣a⃗∣⋅∣b⃗∣↔a⃗\vec{a} \cdot \vec{b} = -|\vec{a}| \cdot |\vec{b}| \leftrightarrow \vec{a} 与 b⃗\vec{b} 的夹角为 π\pi

叉乘

两个三维向量的叉乘运算结果是一个向量.

设有两个三维向量: a⃗=(x1,y1,z1)\vec{a} = (x_1, y_1, z_1), b⃗=(x2,y2,z2)\vec{b} = (x_2, y_2, z_2)

a⃗×b⃗=(y1⋅z2−z1⋅y2,z1⋅x2−x1⋅z2,x1⋅y2−y1⋅x2)\vec{a} \times \vec{b} = (y_1 \cdot z_2 - z_1 \cdot y_2, z_1 \cdot x_2 - x_1 \cdot z_2, x_1 \cdot y_2 - y_1 \cdot x_2)

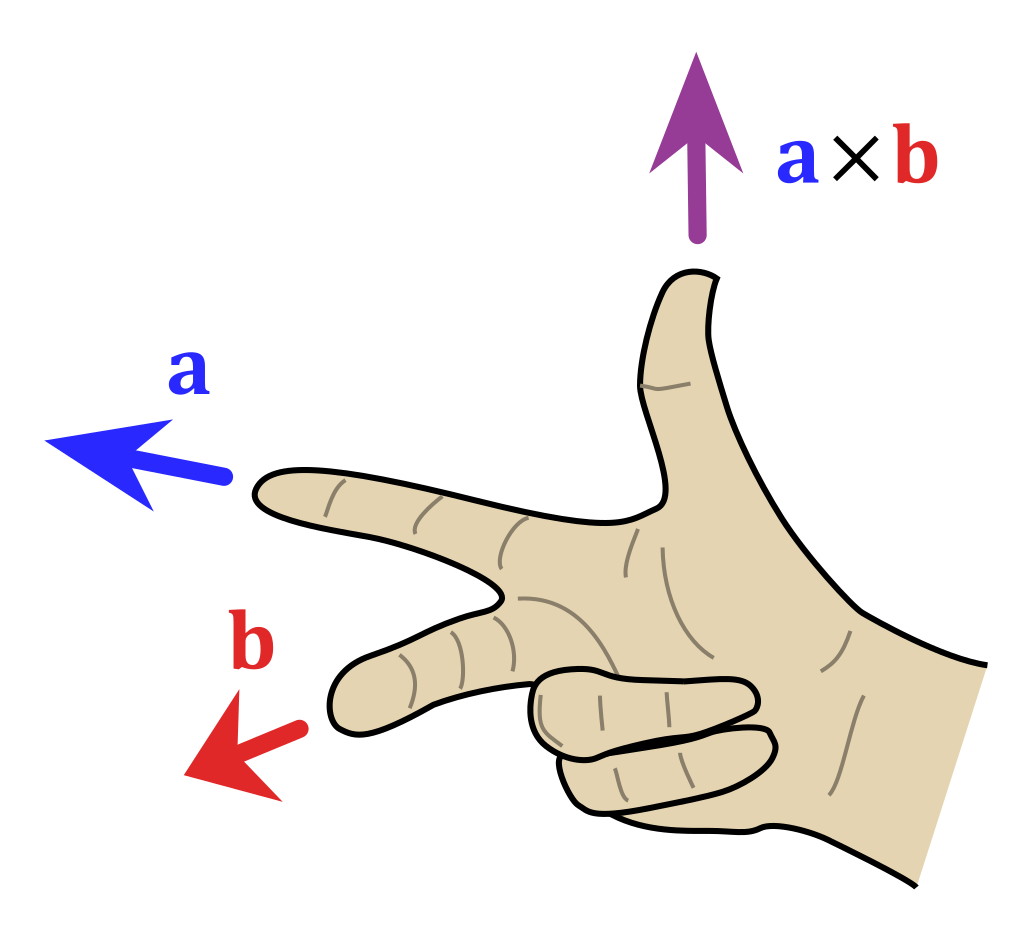
对于两个线性无关的向量 a⃗\vec{a}、b⃗\vec{b}, 叉乘的结果是一个垂直于 a⃗\vec{a}、b⃗\vec{b} 的向量, 其方向由右手定则确定.

两个线性无关的向量是指两个向量不共线, 即两个向量的夹角不为 00 或 π\pi
右手法则

几何中, 叉乘的模长是两个向量构成的平行四边形的面积.

向量叉乘

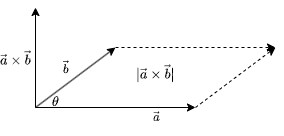
在二维向量中, 叉乘的结果是一个数, 等于两个向量构成的平行四边形的有向面积.

a⃗×b⃗=x1⋅y2−x2⋅y1\vec{a} \times \vec{b} = x_1 \cdot y_2 - x_2 \cdot y_1